1510. Circle through three points

Three points are given on the plane that do not lie on one line. Find the equation of the circle that passes through them. Print the solution in the form

(x – a)² + (y – b)² = r² (1)

and

x² + y² + cx + dy + e = 0 (2)

Input. Each line contains six real numbers A_x, A_y, B_x, B_y, C_x, C_y – the coordinates of three points A(A_x, A_y), B(B_x, B_y), C(C_x, C_y).

Output. For each test case print the equation of a circle in two formats as given in a sample. The values of h, k, r, c, d and e in Equations 1 and 2 are to be printed with three decimal digits. If some of h, k, c, d, e is zero, do not print the corresponding term. Plus and minus signs in the equations should be changed as needed to avoid multiple signs before a number. Plus, minus, and equal signs must be separated from the adjacent characters by a single space on each side. No other spaces are to appear in the equations. Print a single blank line after each equation pair. See output format in example.

Sample input

7.0 -5.0 -1.0 1.0 0.0 -6.0

1.0 7.0 8.0 6.0 7.0 -2.0

Sample output

(x - 3.000)^2 + (y + 2.000)^2 = 5.000^2

x^2 + y^2 - 6.000x + 4.000y - 12.000 = 0

(x - 3.921)^2 + (y - 2.447)^2 = 5.409^2

x^2 + y^2 - 7.842x - 4.895y - 7.895 = 0

SOLUTION

geometry

Algorithm analysis

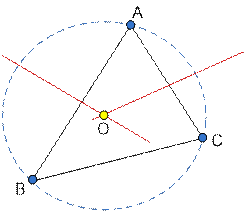
Construct the middle point perpendiculars to the segments AB and AC. The point of their intersection will be the center of the desired circle O. The radius of the circle is equal to the distance OA.

Algorithm realization

Define the constant EPS:

#define EPS 1e-6

Function kramer solves the system of linear equations

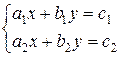
using the Cramer’s method

d = , d_x = , d_y = , x = , y = , d ¹ 0

and returns:

· 0, if the system has a unique solution;

· 1, if the system has no solutions (lines are parallel and do not coincide);

· 2, if the system has an infinite number of solutions (lines coincide);

int kramer(double a1, double b1, double c1,

double a2, double b2, double c2, double &x, double &y)

{

double d = a1 * b2 - a2 * b1;

double dx = c1 * b2 - c2 * b1;

double dy = a1 * c2 - a2 * c1;

if (!d) return (dx == 0.0) + 1;

x = dx/d; y = dy/d;

return 0;

}

Function midperpend using the coordinates of the ends of segment A(x₁, y₁) and B(x₂, y₂) constructs the midpoint perpendicular ax + by + c = 0. Since the vectors AB(x₂ – x₁, y₂ – y₁) and (a, b) are collinear, then

a = x₂ – x₁, b = y₂ – y₁

The midpoint perpendicular passes through the point – the middle of segment АВ, so

ax + by + c = (x₂ – x₁) + (y₂ – y₁) + c = 0,

wherefrom

c =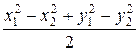

void midperpend(double x1, double y1, double x2, double y2,

double &a, double &b, double &c)

{

a = x2 - x1;

b = y2 - y1;

c = (x1*x1 - x2*x2 + y1*y1 - y2*y2) / 2;

}

The function circle uses three points A(x₁, y₁), В(x₂, y₂) and С(x₃, y₃) to find the center of the circle (xc, yc) and the radius r that passes through them. For this, the perpendiculars to the segments AB and AC are constructed, after which the point of their intersection O is found – the center of the desired circle. The radius r is calculated as the distance between points O and A.

void circle(double x1, double y1, double x2, double y2, double x3,

double y3, double &xc, double &yc, double &r)

{

double a1,b1,c1,a2,b2,c2;

midperpend(x1,y1,x2,y2,a1,b1,c1);

midperpend(x1,y1,x3,y3,a2,b2,c2);

kramer(a1,b1,-c1,a2,b2,-c2,xc,yc);

r = sqrt((x1 - xc)*(x1 - xc) + (y1 - yc)*(y1 - yc));

}

The main part of the program. Read the input data.

while(scanf("%lf %lf %lf %lf %lf %lf",

&x_1,&y_1,&x_2,&y_2,&x_3,&y_3) == 6)

{

For each test find the center (xc, yc) and the radius r of the circle that pass through three points.

circle(x_1,y_1,x_2,y_2,x_3,y_3,xc,yc,r);

Print the equation of a circle in the form (x – a)² + (y – b)² = r².

if (fabs(xc) < EPS) printf("x^2"); else

{

printf("(x");

if (xc >= 0.0) printf(" - "); else printf(" + ");

printf("%.3lf)^2",fabs(xc));

}

printf(" + ");

if (fabs(yc) < EPS) printf("y^2"); else

{

printf("(y");

if (yc >= 0.0) printf(" - "); else printf(" + ");

printf("%.3lf)^2",fabs(yc));

}

printf(" = %.3lf^2\n",r);

Print the equation of a circle in the form x² + y² + cx + dy + e = 0.

printf("x^2 + y^2");

if (fabs(xc) > EPS)

{

if (xc > 0.0) printf(" - "); else printf(" + ");

printf("%.3lfx",2*fabs(xc));

}

if (fabs(yc) > EPS)

{

if (yc > 0.0) printf(" - "); else printf(" + ");

printf("%.3lfy",2*fabs(yc));

}

r1 = xc*xc + yc*yc - r*r;

if (fabs(r1) > EPS)

{

if (r1 > 0.0) printf(" + "); else printf(" - ");

printf("%.3lf",fabs(r1));

}

printf(" = 0\n\n");

}